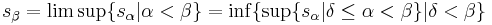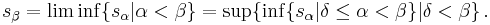Continuous function (set theory)
In mathematics, specifically set theory, a continuous function is a sequence of ordinals such that the values assumed at limit stages are the limits (limit suprema and limit infima) of all values at previous stages. More formally, let γ be an ordinal, and 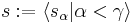 be a γ-sequence of ordinals. Then s is continuous if at every limit ordinal β < γ,
be a γ-sequence of ordinals. Then s is continuous if at every limit ordinal β < γ,
and
Alternatively, s is continuous if s: γ → range(s) is a continuous function when the sets are each equipped with the order topology.
References
- Thomas Jech. Set Theory, 3rd millennium ed., 2002, Springer Monographs in Mathematics,Springer, ISBN 3-540-44085-2